Next: Grid-based clustering with adaptive Up: Fast Two-Step Histogram-Based Image Previous: Related work
Each density attractor of PDF delineates associated basin of attraction, a
set of points
![]() for which hill-climbing procedure
started at
for which hill-climbing procedure
started at ![]() converges to
converges to ![]() .
Hill-climbing procedure can be guided by a gradient of PDF
[23,24] or step-wise [22].
.
Hill-climbing procedure can be guided by a gradient of PDF
[23,24] or step-wise [22].
Kernel density estimation [25] is a PDF estimation method based on the concept that the density function at a continuity point can be estimated using the sample observation that falls within a region around that point.
Let
![]() be a set of
be a set of ![]() data samples in
data samples in ![]() -dimensional
vector space
-dimensional
vector space
![]() , and
, and
![]() , a radially symmetric kernel satisfying
, a radially symmetric kernel satisfying
The shape of the PDF estimate is strongly influenced by the bandwidth ![]() ,
which defines the scale of observation. Larger values of
,
which defines the scale of observation. Larger values of ![]() result in smoother density estimate, while for smaller values the contribution
of each sample to overall density has the emphasized local character,
resulting in density estimate revealing details on a finer scale.
The fixed bandwidth
result in smoother density estimate, while for smaller values the contribution
of each sample to overall density has the emphasized local character,
resulting in density estimate revealing details on a finer scale.
The fixed bandwidth ![]() , constant across
, constant across
![]() , affects the
estimation performance when the data exhibit local scale
variations. Frequently more smoothing is needed in the tails of the
distribution, while less smoothing is needed in the dense regions.
, affects the
estimation performance when the data exhibit local scale
variations. Frequently more smoothing is needed in the tails of the
distribution, while less smoothing is needed in the dense regions.
Underlying data distribution can be more accurately described using the
variable bandwidth kernel.
By selecting a different bandwidth ![]() for each sample
for each sample ![]() , the
sample point density estimator [5,26] is defined:
, the
sample point density estimator [5,26] is defined:
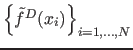 .
.
Damir Krstinic 2011-11-04